Alumnus of AIT.

Alumnus of Coastal Carolina University.

Prof. Ashay Dharwadker's Courses (3):

Course	Semester	Grade	Add New Course
Probability & Statistics	Spring 2003	View	Update Course
Algorithm Design - I	Fall 2002	View	Update Course
Algorithm Design - II	Spring 2004	View	Update Course

Projects (1)

The first (and probably the most important) thing that any computer programmer learns are the various algorithms for SORTING data. They are absolutely critical for a complete understanding of the whole computer science field itself.

But it can get quite confusing at times. Especially, when one wants to understand how each one of them works? Or, How each one of them is different from the other? We think we have an answer to that. Suppose you wish to introduce somebody to the game of FOOTBALL. A verbal discription would not be very helpful. The best solution would be to show a visual of the football game to that person.

Same is the case with Sorting Methods. Through this project, we give a visual discription of the various Sorting Algorithms, with the aim of making learning easy and fun.

But the solution also gives rise to a more complex problem. How do we represent the sorting algorithms visually. The solution is to create unique visualization schemes to represent the status of data elements at various instances of time.

This method of representation gives rise to a more complex field in mathematics known as Dynamical Systems.

After the main idea of the project was concieved, the elements of the project were distributed to the various team members.

Team Members:
• Karan Sahni (Algorithms - Coding Sorting Algorithms into C++ Programs)
• Parul Yadav (Visualizations - Creating Visualization Schemes in OpenGL)
• Devina Sibal (Visualizations - Creating Visualization Schemes in OpenGL)
• Prakash (Win32 Integration - Integrating all components in Visual C++ Environment)

Seminars (0)

Research Notes (2)

Applications: Hashing has got a lot of applications in the real world: One is searching in database which has been discussed earlier. Hashing is used in cryptography. The basic requirements for a cryptographic hash function are as follows: The input can be of any length. The output has a fixed length. H(x) is relatively easy to compute for any given x. H(x) is one-way. H(x) is collision-free. A hash function H is said to be one-way if it is hard to invert, where "hard to invert'' means that given a hash value h, it is computationally infeasible to find some input x such that H(x) = h. If, given a message x, it is computationally infeasible to find a message y not equal to x such that H(x) = H(y), then H is said to be a weakly collision-free hash function. A strongly collision-free hash function H is one for which it is computationally infeasible to find any two messages x and y such that H(x) = H(y). The hash value represents concisely the longer message or document from which it was computed, this value is called the message digest. The main role of a cryptographic hash function is in the provision of message integrity checks and digital signatures. Now what actually happens in this case is basically the digital signature or integrity check of some document is computed by applying the cryptographic processing to the documents’hash value,which is small compared to the documents itself. Hence in this way a digest can be revealed without actually showing the document from which it is derived. 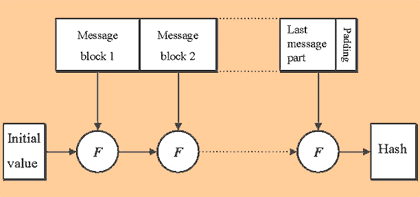Damgård and Merkle greatly influenced cryptographic hash function design by defining a hash function in terms of what is called a compression function. A compression function takes a fixed-length input and returns a shorter, fixed-length output. Given a compression function, a hash function can be defined by repeated applications of the compression function until the entire message has been processed. In this process, a message of arbitrary length is broken into blocks whose length depends on the compression function, and ``padded'' (for security reasons) so the size of the message is a multiple of the block size. The blocks are then processed sequentially, taking as input the result of the hash so far and the current message block, with the final output being the hash value for the message.

Reference: http://whatis.database.search.co

The algorithm requires a surface representation for both the ligand and the receptor. The surfaces are represented by critical points, accurately and sparsely placed, at key locations on the molecular surface.

In the algorithm, there are two phases, as before: In the preprocessing phase, the ligand molecules are preprocessed, and their geometrical information is encoded in the hash table. Then, in the recognition phase, the features of the receptor are used to obtain an index to hash table, and the corresponding entries in the hash table receive a vote. At the end of the process, the ligand molecules that receive the highest number of votes can be selected for a more careful analysis.

References :

• Efficient Computational Algorithms for Docking, and for Generating and Matching a Library of Functional Epitopes I. Rigid and Flexible Hinge-Bending Docking Algorithms. Ruth Nussinov, and Haim J. Wolfson. Combinatorial Chemistry & High Throughput Screening, 2, 277-287, (1999).
• Geometric Hashing: An overview. Haim J. Wolfson, Isidore Rigoutsos. IEEE Computational Science and Engineering, 1997, pp. 10-21