| Home | Sign up! | Projects | Seminars | Research Notes | Today's Lecture | About |
Prateeti RajEmail
prateeti_r@rediffmail.com
| Profile: Other courses: Advanced Developers Curicullum (ADC) certificate course from IBM.
Post Graduation: Currently pursuing MS(IS) from Texas, U.S.A.
I am also working as Graduate Research Assistant.
Hobbies: Drawing, Playing synthesizer, Dancing and Reading books.
Interests in Computers: I like to do programming, no specific language is my favorite as I feel they are more or less the same. What interests me is the work I am doing should be exciting. I also have a keen interest towards upcoming areas like Artificial Intelligence, Neural Networks (that is what motivated me to do my project work on the same), Data Mining, Data Warehousing, Robotics etc. I also like Software Engineering and find it to be very interesting. I would further like to hone my skills in the above mentioned areas and try to discover new thing as I feel this field is still untapped and a lot can be learnt & discovered. This is what always keeps me going and keeps on increasing my curosity to learn new things!
Neural Networks
Master’s Thesis
by
Prateeti Raj
Thesis Supervisor
Prof. Ashay Dharwadker
15th April 2004
Abstract
This thesis is a survey of the field of Neural Networks. Various types
of neural networks and learning algorithms are explained and demonstrated.
In particular, the Perceptron, Hamming and Hopfield networks and their
applications are described, and a detailed historical background is provided.
The mathematical model of a Threshold Logic Unit and the problem of finding
a linearly separable function that agrees with the desired training set
is explored. Consequently, a calculus argument in the weight space allows
us to derive the famous Widrow-Hoff delta rule using the zero-one step
function and the Werbos generalized delta rule using the sigmoid function.
We have implemented all of these neural networks and learning algorithms
in C++ and provide the source code of the software under the GNU public
license for noncommercial use on the accompanying CD.
Contents
1. The Human Brain
2. History of Neural Networks
3. What is a Neural Network?
4. Learning in a Neural Network
5. A Simple Example of a Neural Network
6. Problem Statement
7. Perceptron
8. Pattern Recognition Problem
9. Programs
10. Hamming Network
11. Program on Hamming Network
12. Hopfield Networks
13. Widrow-Hoff Algorithm
14. Program using Widrow-Hoff Algorithm
15. Werbos Algorithm
16. Summary of Presentations Given
17. Applications of Neural Networks
18. References |
Prof. Ashay Dharwadker's Courses (3): | Course | Semester | Grade | | | MS Project | Fall 2003 | View | | | Database Systems | Fall 2003 | View | | | Computer Networks | Spring 2004 | View | |
|
Project ID: 12
Course: MS Project
Topic: Neural Networks
| | Description: I am designing a neural network that will sort a fruit or vegetable when it is brought to the warehouse. The fruits will be loaded on a conveyer belt in a warehouse. This conveyer passes through a set of sensors. These sensors measure three properties of the fruit:shape, texture and weight. The shape texture will output a 1 if the fruit is approximately round and a -1 if it is more elliptical. The texture sensor will output a 1 if the surface of the fruit is smooth and a -1 if it is rough. The weight sensor will output a 1 if the fruit is more than one pound and a -1 if it is less than one pound.
The three sensors are then input to a neural network. The neural network will then decide which fruit is on the conveyer belt so that it can be directed to the correct storage bin. There are two kinds of fruits: apples & oranges.
Apple/Orange Sorter
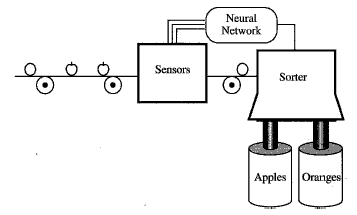
Reference: What is a Neural Network?
|
Project ID: 16
Course: Database Systems
Topic: Cricket Plus!
| | Description: I am making a project with Srijani Kirti. We are making a database that would contain information about the cricket players of different countries, their profiles, data about them like higest score, test average, one day average, no. of centuries, half centuries etc. One can see the individual score card on the web page of the cricketer of their choice of the respective country.
I am stating the sql syntax used to create our relational database for Cricket Plus!
mysql>create database cricketplus;
mysql>use database cricketplus;
mysql>create table countries(country_name char(40) not null, uniform_color char(40), cricket_board char(40), famous_playgrounds char(40), world_cups_won integer);
mysql>create table cricket_players(player_id integer not null, player_name char(40), highest_score integer, average integer, no_of_centuries integer, no_of half_centuries integer, bowling_average integer, wickets_taken integer);
mysql>create table country_players(player_id char(40) not null, country_name char(40) not null, name char(40) not null, primary key(player_id, country_name), foreign key (country_name) references countries);
|
Seminar ID: 7
Course: MS Project
Topic: Neural Networks
| Description:
Seminar 1: I have given a seminar on Neural Networks in which I explained the neural network, its history and also about the different types of neural networks. I also talked about my project and explained how the neural network will sort the apple & oranges. The exciting part of the seminar was that we found out that Turing Machines are actually Recurrent Neural Networks. I also talked about the various applications in which neural networks are used. |
Seminar ID: 46
Course: MS Project
Topic: Neural Networks
| Description:
Seminar 2: I gave a seminar on Hamming Networks and talked about the Feedforward and Recurrent layers. I also explained how Hamming Networks work in context to my orange/apple sorter. |
Research Note ID: 18
Course: MS Project
Topic: Neural Network
| Description:
Research Note : I am currently studying the different networks that can be used to solve our problem. They are:
- Feedforward Networks (perceptron)
- Competitive Networks (Hamming Network)
- Recurrent Associative Networks (Hopfield Network)
I have developed a program for the perceptron network and am trying to develop similar programs for the Hamming & Hopfield Networks.
|
Research Note ID: 20
Course: Database Systems
Topic: Pattern Recognition using SQL
| Description:
Pattern Recognition using SQL
LIKE 'pattern'
The pattern can contain wild card characters - % (percentage) and (underscore). The % is used to denote any number of unknown characters and _ denotes one unknown character. To denote more than one unknown character using _, the number of _ must be equal to the number of unknown characters.
- To retreive rows where the state name begins with K and followed by any other character. Example, KARNATAKA, KERALA
SELECT FIRST_NAME, LAST_NAME, STATE
FROM CUSTOMER WHERE STATE LIKE 'K%';
- To retreive rows where the first name contains the word RAJ embedded in it.
Example, RAJESH, DEVRAJ, RAJESHWARI.
SELECT FIRST_NAME, LAST_NAME, STATE
FROM CUSTOMER WHERE FIRST_NAME LIKE '%RAJ%';
- To retreive rows where the ADD2 contains the word TEXAS or TEXIS in which the 3rd character may be anything. This is done using the underscore.
SELECT FIRST_NAME, LAST_NAME, ADD2, STATE
FROM CUSTOMER WHERE ADD2 LIKE 'TEX_S';
|
Research Note ID: 22
Course: Database Systems
Topic: Number Functions in SQL
| Description:
Number Functions in SQL
- ABS(data): Returns the absolute value of data (i.e. positive value).
SQL>SELECT ABS(-5000) FROM DUAL;
=5000
- CEIL(data): Returns the smallest integer greater than or equal to data.
SQL>SELECT CEIL(123.55) FROM DUAL;
=124
- FLOOR(data): Returns the largest integer less than or equal to data.
SQL>SELECT FLOOR(123.55) FROM DUAL;
=123
- LN(data): Returns the natural algorithm of data.
- LOG(b,data): Returns the base 'b' logarithm of data.
- MOD(data,Y): Returns the modulus of dividing data by Y.
SQL>SELECT MOD(101,2) FROM DUAL;
=1
- POWER(data,Y): Returns the data raised to the POWER of Y.
SQL>SELECT POWER(2,4) FROM DUAL;
=16
- ROUND(data,n): Where n is the number of decimal places to which the data is rounded.
SQL>SELECT ROUND(123.55), ROUND(123.55,1)
FROM DUAL;
124 123.6
- SQRT(data): Returns the square root of data.
SQL>SELECT SQRT(64) FROM DUAL;
=8
- TRUNC(data,n): Where n is the number of decimal places for truncation.
SQL>SELECT TRUNC(123.55,0), TRUNC(123.55,1)
FROM DUAL;
123 123.5
|
Research Note ID: 29
Course: Database Systems
Topic: SQL VIEWS
| | Description: SQL Views: Views are logical tables of data extracted from existing tables. It can be queried just like a table, but does not require disk space. It can be thought of as either a virtual table or a stored query. Also the data accessible through a view is not stored in the database as a distinct object. What is stored in the database is a SELECT statement. The result set of the SELECT statement forms the virtual table returned by the view.
Use of View
- It can be used to hide sensitive columns. To do this the owner of the view must grant the SELECT privilege on the view and revoke the privileges on the underlying tables.
- It can be used to hide complex queries involving multiple tables. Users need not concern with the syntax of complex queries.
- Views are created with a Check option, prevents the updating of other rows and columns.
To Create a View
Syntax: CREATE or REPLACE VIEW view-name AS query;
Example: CREATE VIEW EMP_VIEW AS
SELECT emp_no, emp_name from emp;
Note:The ORDER BY clause cannot be used in a Create View statement.
To Display the View
Syntax: SELECT * FROM VIEW_NAME;
Example: SELECT * FROM EMP_VIEW;
To View the Columns in a View
Syntax: DESC VIEW_NAME;
Example: DESC EMP_VIEW;
To Delete a View
Syntax: DROP VIEW VIEW-NAME;
Example: DROP VIEW EMP_VIEW;
Updating a View
VIEW cannot be updated if it contains,
- joins
- set operators (UNION, INTERSECT, MINUS)
- GROUP functions
- Group by Clause
- DISTINCT
With Check Option The CHECK OPTION will validate the data during an INSERT or UPDATE into a VIEW.
Example:
CREATE OR REPLACE VIEW EMP AS
SELECT * FROM CUSTOMER
WHERE CITY = 'BANGALORE' WITH CHECK OPTION;
Check option will validate data during input or update based on the constraint, i.e. CITY='BANGALORE'. When a row is inserted into view EMP, CITY has to be 'BANGALORE'. Similarly when a row is updated, the value in column CITY has to be 'BANGALORE',
INSERT on a VIEW is allowed. If the VIEW does not contain all the columns in the base table, then the missing columns can be specified as Null, unless it is the Primary Key.
SQL>SELECT * FROM USER_VIEWS;
Will list the text of the views created by the user. USER_VIEWS is a data dictionary table.
|
Research Note ID: 57
Course: Computer Networks
Topic: Wide Area Networks
| Description: A wide area network is a computer network that spreads across a region, a whole country or even the whole world. WANs interconnect LANs located in any part of the world. It spans a large geographical area like a country or a continent. It contains a collection of machines called hosts that run user(i.e. application programs). The LANs are connected with the help of WAN backbones. Generally WANs use satellites as the primary transmission on media and, therefore, the transmission is comparatively costly. Where LAN market has grown at the rate of 175%, the WAN growth has been relatively slow at 4)%. The popular, WAN protocols are: X.25, Frame Relay, and ATM(asynchronous transmission mode). The protocols stated are explained briefly below:
X.25 Protocol: This protocol is a low bandwidth transmission protocol with 50kbps data transfer rate. It was earlier used by most of the WANs.
Frame Relay: The Frame Relay is a high bandwidth protocol with 56kbps to 45Mbps data transfer rate. In fact, this is a stream lined version of X.25 protocol that assumes reliable communication links. It is a very cost effective transmission protocol and is very popular within Networking companies.
ATM: It is an extremely fast transmission protocol with bandwidth as high as 622Mbps. It is also designed to handle integrated data, voice, and video transmission. This protocol is gaining popularity world wide because it can handle both video and multimedia applications.
Example: DHLNET uses both X.25 and Frame Relay technology to connect the various LANs of its offices world over.
Indian Networks The popular WAN installations in India are Nicnet, I-Net, Calibnet, coalnet, ERNET(Education and Research Network), Sail net and Star net.
The salient features of ERNET are given below:
1. This network is primarily meant for promotion of information exchange among the various educational and research institutes such as IITs, IISc, DOE etc.
2. Common services provided by this network are:
(i) file transfer
(ii) data bases access
The ERNET Architecture is shown below:
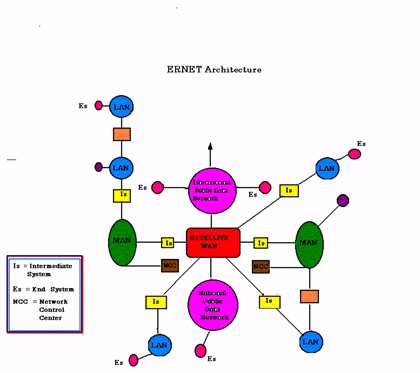 |
Research Note ID: 68
Course: MS Project
Topic: Neural Networks
| Description: Research Note :
- Perceptron
- Feedforward Network
- Linear Decsion Boundary
- One Neuron for Each Decision
- Hamming Network
- Competitive Network
- First Layer: Pattern Matching (Inner Product)
- Second Layer: Competition (Winner-Take-All) #Neuron=#Prototype Patterns
- Hopfield Network
- Dynamic Associative Memory Network
- Network Output Converges to a Prototype Pattern
- #Neurons=#Elements in each Prototype Pattern
|
Research Note ID: 69
Course: MS Project
Topic: Neural Networks
| Description: Research Note :
During the seminar I mentioned that Neural Networks can be used for universal computation & universal approxiamation. Later, we found out that Turing Machines are Recurrent Neural Networks as any algebraically computable function can be expressed as a recurrent neural network structure consisting of identical computing elements.
Anyone interested can go to the following link to see the research paper Turing Machines are Recurrent Neural Networks
|
Research Note ID: 70
Course: MS Project
Topic: Neural Networks
| Description: Research Note :
I have developed the program for Hamming network and am studying Hopfield Networks currently. I am also studying the research paper given by Ashay Sir which is very interesting.
|
Research Note ID: 71
Course: MS Project
Topic: Widrow Hoff (Neural Networks)
| | Description: Boolean functions f that are implemented by a Threshold Logic Unit (TLU). We have the following equation
f(x)=w1x1+w2x2+……………….+wnxn.
This function is a linearly separable function. For machines with only two actions 0,1 TLU’s suffice. For more complex actions 0,1,2 need a network of TLU’s which is called a Neural Network.
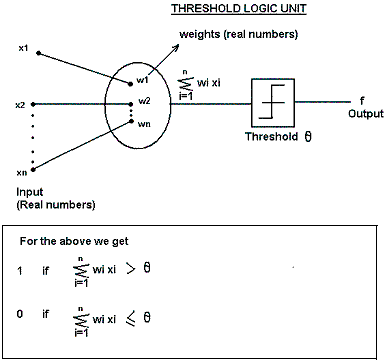
Example:
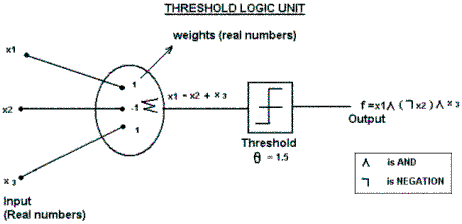
How can a machine Learn
Inputs Desired Output
X1=(x1+x2+……….+xn) d1
X2=(x1’+x2’+………..+xn’) d2
.
.
.
.
Xk=(x1k+x2k+………..+xnk) dk
Objective: To find function “f” such that f(Xi)=di for i=0,1,2,3…….,k.
Experimental evidence suggests that if the training set is “typical” then f will generate approximately correct response for all x.
Frank Rosenblatt, Widrow and Hoff gave the following in 1962.
Consider a single TLU
Weights W = (W1, W2,…….,WN)
Threshold theta (Assume theta =0)
X.W=X.W1+X2.W2+……..XN.WN
Input X = (x1,x2,…..,xn)
Output = {1 if X.W> theta
0 if X.W<= theta
Calculus in the weight space
Start with arbitrary
W=(W1,W2….,WN)
(X=X1 In the training set)
Define error € = (f(x)-d)2
Define gradient d€/dw = (d€/dw1, d€/dw2,…..d€/dwn)
Define S=X.W
= ds/dw = x
Chain Rule
d€/dw = d€/ds.ds/dw => d€/ds.x
But d€/ds = (f(x) – d) .df/ds
So d€/dw = 2(f(x)-d)df/ds . x
Aim: To minimize €
Use Method of Steepest Descent
(moves w along the steepest negative gradient)
Problem: What is df/ds?
Widrow Hoff Algorithm
Assume we want to adjust the weights so that
If f(x) = 1 =d => x.w=1
If f(x) = 0 = d => x.w = -1
Then f=s
€ = (f – d)2 => df/ds = 1
So now, d€/dw = 2(f-d)x
Steepest Descent Method
Step 1: Start with arbitrary w
Step 2: Replace w by w = (f-d)x
Where c = learning rate parameter
Repeat step 2 until w converges
This is Widrow Hoff Algorithm
X=(1,1,0)
W=(0,0,0)
F(x)=1
w1.1+w2.1+w3.0 = 1
0.5(1) + 0.5 (1)+(0 or 1) 0 = 0.5+0.5+0=1
The output of the values will converge to 0.5 with the iterations from 0 to 0.5.
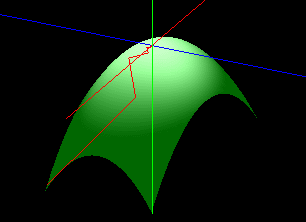
Generalized Delta Rule Here Wi+1 = Wi + c(d-f).f(1-f)x
Where f = 1/1+e-s(e to the power -s)
|
Research Note ID: 77
Course: MS Project
Topic: Turing Machines and Recurrent Neural Networks
| Description:
Turing Machines and Neural Networks
Who was Alan
Turing
Alan Turing was the founder of computer science,
mathematician, philosopher, code breaker and a visionary.
He was born in 1912 (23 June) at Paddington, London. He studied at the
Sherborne School, during 1926-31. He was then an undergraduate student
at King’s College, Cambridge University during 1931-34. In 1935 he was
elected Fellow of King’s College, Cambridge for his work in Quantum
mechanics, probability and logic during 1932-35. Before the advent of
the digital computer i.e. in the 1930's several mathematicians began to
think about what it means to be able to compute a function.
Turing's definitive contribution was the relation between logical
instructions, the action of the mind, and a machine which could in
principle be embodied in a practical physical form. Thus, in 1936, he
contributed ‘The Turing machine, computability, universal machine’. At
the same time American logician, Alonzo Church had also been working on
the same and came with a parallel conclusion. It was seen, however that
Turing's approach was original and different; Church relied upon an
assumption internal to mathematics, rather than appealing to operations
that could actually be done by real things or people in the physical
world. Alonzo Church and Alan Turing independently arrived at
equivalent conclusions. As we might phrase their common definition now:
A function is computable if it can be computed by a Turing
machine.
What is a Turing
Machine
Logically a Turing machine has all the power of any digital computer.
Conceptually a Turing machine processes an infinite tape which is
divided into squares, any square of which may contain a symbol from a
finite alphabet, with the restriction that there can be only finitely
many non-blank squares on the tape. At any time, the Turing machine has
a read/write head positioned at some square on the tape. Furthermore,
at any time, the Turing machine is in any one of a finite number of
internal states. The Turing machine is further specified by a set of instructions of the following form:
(current_state, current_symbol, new_state, new_symbol, left/right)Turing expanded this idea to show that there exists a "universal" Turing machine, a machine which can calculate any number and function, given the appropriate instructions. The set of instructions can be thought of as a program for the Turing machine.
Turing’s Paper, On Computable Numbers was published near the end of 1936.This paper generated a lot of attention for him and the idea came to mathematician John Von Neumann. Turing obtained his Ph.D thesis through work that extended his original ideas i.e. during 1936-38
Turing also completed his Ph.D. in Logic, algebra, number theory at Princeton University.
Reference: http://www.turing.org.uk/bio/part3.html
http://www.nmia.com/~soki/turing/
http://www.ams.
org/new-in-math/cover/turing.html
It is found that Recurrent Neural Networks are actually equivalent to Turing Machines i.e. they can compute any algebraically computable function.
Heikki Hyötyniemi of Helsinki University of Technology, Control
Engineering Laboratory, Otakaari 5A, FIN-02150 Espoo, Finland has published a paper stating the same i.e. ‘Turing Machines are Recurrent
Neural Networks’.
The paper can be viewed at the following link:
http://www.uwasa.fi/stes/step96/step96/hyotyniemi1/
Explanation: One can use Neural networks for classification tasks,
telling whether an input pattern belongs to a specific class or not. It has been known for a long time that one-layer feedforward networks (i.e
a single Threshold Logic Unit) can be used to classify only patterns that are linearly separable (linearly separable functions). However, the more there are successive layers, the more complex the distribution of the classes can be.
In a Recurrent Neural Network we have two layers: Feed forward Layer and Recurrent Layer. When feedback is introduced in the network structure, so that perceptron output values are recycled, the number of successive layers becomes, in principle, infinite. So now is the computational power enhanced qualitatively? The answer is yes.
In this paper, it is shown that a recurrent network structure consisting of identical computing elements can be used to accomplish
any (algorithmically) computable function.
Then Recurrent Neural Networks are capable of doing all that a Turing Machine can do.
P and NP Problem
P Problem
The class P informally is the class of decision problems that can be solved by some algorithms within a number of steps bounded by some
fixed polynomial in the length of the input. We can get an exact solution to those problems within some reasonable amount of time. Such
problems fall in class P where P stands for polynomial time complexity.
Problems for which there is a polynomial time algorithm are called tractable.
To define the problem in a precise way it is necessary to give a formal
model of a computer. The Turing machine is the standard computer model
in computability theory which was introduced by Alan Turing in 1936.
The model was introduced before physical computers were built; but it
still continues to be accepted as the proper computer model for the
purpose of defining computable function.
NP Problem
There is another class of problems that are intractable, for which we
currently have no algorithm that will solve the problems in any
reasonable amount of time. These problems fall in the class NP, which
means nondeterministic polynomial time complexity. Only deterministic
algorithms that are known to solve these problems have a complexity
that is of exponential or factorial order. For some problems, the complexity is given by 2N, where N is equal to the number of input values. In this case, each time we add one additional input value, the
amount of time required by the algorithm to solve the problem doubles.
Example: If an algorithm computes 512 operations(that is 29) to solve a problem that has 9 elements, it would take 1024 operations to solve a problem that has 10 elements.
NP is not the same as non-P. NP which means “nondeterministic
polynomial time” was originally defined in terms of nondeterministic
machines (that is, machines that have more than one possible move from
a given configuration).
Thus a NP class contains problems if they can be solved in polynomial
time by a nondeterministic Turing machine (a nondeterministic Turing
machine means a "parallel" Turing machine which can simultaneously take
many computational paths, but have the restriction that these parallel
Turing machines cannot communicate).
A P problem (whose solution time is bounded by a polynomial) is always
NP also. If a problem is known to be NP, and a solution to the problem
is somehow known, then demonstrating the correctness of the solution
can always be reduced to a single P (polynomial time) verification. If
P and NP are not equivalent, then the solution of NP-problems requires
(in the worst case) an exhaustive search. An Exhaustive search means it
might be required to test each possibility sequentially for discrete
problems in which no efficient solution method is known, in order to
determine if it is the solution. Such exhaustive examination of all
possibilities is known as exhaustive search, direct search, or the
"brute force" method (that is checking all the possibilities, like in
Hamiltonian circuits which yet have no known algorithms for finding a
Hamiltonian circuit).
NP-Hard Problem
A problem is NP-hard (Non-deterministic Polynomial-time Hard) if
solving it in polynomial time would make it possible to solve all
problems in class NP in polynomial time. That is, a problem is NP-hard
if an algorithm for solving it can be translated into one for solving
any other NP problem (nondeterministic polynomial time) problem.
NP-Complete Problem
NP Complete are the hardest problems in the class NP. Such problems are
singled out because if at any point we find a deterministic polynomial
time algorithm for one of them, all of the problems in NP must have
deterministic polynomial time algorithms.
Use of Neural Networks to solve P, NP, NP Hard and NP Complete
problems
The Turing Machines can be used in computing P and NP problems. So the
Recurrent Neural Networks can also be used for the same.
However, both Hopfield and Recurrent Neural Networks are used for
solving problems that deal with P and NP complexities.
The maximum clique problem (MCP) is a classic graph optimization
problem with many real-world applications. This problem is NP-complete
and computationally intractable even to approximate with certain
absolute performance bounds. New discrete competitive Hopfield neural
network for finding near-optimum solutions for the MCP are used. More
information related to this topic can be obtained at the following
address:
h
ttp://portal.acm.org/citation.cfm?id=775532&dl=ACM&coll=GUIDE
Thus, Recurrent Neural Networks can be used for Universal Computation
and Universal Approximation that is all places here Turing Machines
can be used.
Universal Approximation: It means having the
ability to approximate any function to an arbitrary degree of
accuracy.
Universal Computation: It means the ability of computing
anything that can be computed in principle, that is equivalent in
computing power to a Turing machine, the lambda calculus, or a Post
production system. |
|
Last updated on Monday, 12th May 2008, 03:11:38 PM.
Prof. Ashay Dharwadker
|
|

