| Home | Sign up! | Projects | Seminars | Research Notes | Today's Lecture | About |
Gunjan SharmaEmail
gingunjan@yahoo.com
| Profile: I am studying for my Bachelor’s degree in Computer Information Systems as a sophomore at AIT affiliated to Tarleton State University, Texas. My main interests in Computer Science are in the areas of design of databases, Data Warehousing and Artificial Intelligence. My skills include Windows Programming using C++ and MFC, designing MySQL and Oracle databases with web based PHP and ASP programming. I have worked as Personal Relations Manager in an Event Management Company for three and a half months.
I like reading novels (romantic and inspirational), listening to music, collecting cigarettes(though I dislike smokers) and writing poetry.
Prof. Ashay Dharwadker's Courses (2): | Course | Semester | Grade | | | Information Systems | Fall 2003 | View | | | Database Systems | Fall 2003 | View | |
|
Project ID: 7
Course: Database Systems
Topic: NBA (National Basketball Association)
| | Description: Group Partner:- Sudeep Tomar
We have started working on a database including the teams,players,scheduled of upcoming matches and complete player's profile of the game, Basketball.This is going to be a huge and vast database.Well we are very excited about the project. We are also thinking of building up our own internet browser. |
Seminar ID: 5
Course: Information Systems
Topic: Turing Machines
| Description: (With Sudeep Tomar) We talked about the computer scientist, mathematician and visionary Alan Turing. We explained the concept and demonstrated an actual Turing Machine for Addition (C++ source code was provided by Ashay Sir). The following picture shows the Turing Machine for Addition. The blue squares form the tape, the yellow square is the portion of the tape being scanned, the symbols for the computation are I, X and the black square displays the current state of the machine. The computation being performed is one plus one equals two!
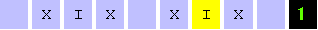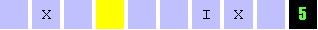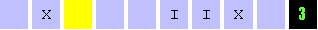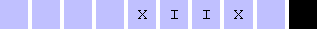
It is important to stress that a Turing Machine is an abstract concept of a computational device. Church's Thesis, which most computer scientists accept, is that any possible computation can be performed by some Turing Machine. The number of steps that the Turing Machine takes to perform the computation, as a function of the input size, measures the complexity of the computation. |
Research Note ID: 14
Course: Information Systems
Topic: Alan Turing and Turing Machines
| Description: We (Sudeep Tomar and I) gave a seminar on Turing Machines, which involved a great amount of research on the topic.A small introduction of the Machine and the scientist himself is written below.
Alan Mathison Turing was born in London, 23 June 1912. Turing studied mathematics with increasing distinction at King's College, Cambridge University, and was elected a Fellow of the college in 1935.
His first paper "On Computable Numbers…" (Turing 1936-7) gave a definition of computation and an absolute limitation on what computation could achieve, which makes it the founding work of modern computer science. From 1939 to 1945 Turing was almost totally engaged in the mastery of the German enciphering machine, Enigma, and other crypto logical investigations at now-famous Bletchley Park, the British government's wartime communications headquarters.
# Turing also labored under the disadvantage that his wartime achievements remained totally secret. His ideas led the field in 1946, but this was little recognized. Frustrated in his work, he emerged as a powerful marathon runner, and almost qualified for the British team in the 1948 Olympic Games.
Turing Machine
A Turing machine is an abstract representationof a computing device. It is a one dimensional (bi-directional) tape divided into squares which has a read/write head which scans the squares each of which is inscribed with a 0 or a 1. The behavior of the tape (i.e. of scanning the square, erasing what it finds there, printing 0 or 1 and then moving on to another square) is completely determined by three parameters: (1) the state the machine is in, (2) the number on the square it is scanning, and (3) a table of instructions.
It was just a preview, to learn more about the scientist, his contribution or the machines the links below are really rich in their content. We have taken information from the following websites:
- 1."Turing Machine", The Stanford Encyclopedia of Philosophy (Summer 2003 Edition), Edward N. Zalta (ed.), URL = http://plato.stanford.edu/archives/sum2003/entries/turing-machine
- 2. "Alan Turing", The Stanford Encyclopedia of Philosophy (Summer 2002 Edition), Edward N. Zalta (ed.), URL = http://plato.stanford.edu/archives/sum2002/entries/turing.
# We (Sudeep and I) are also planning to give a seminar on Enigma Cipher. The processing of the topic is still going on. You can view some of the research done on the above subject in Sudeep’s Profile under Research Work.
|
Research Note ID: 35
Course: Information Systems
Topic: Turing Test
| Description: The Turing Test was developed during the 1950's Alan Turing. Basically, it is a test for Artificial Intelligence. Turing concluded that a machine could be seen as being intelligent if it could "fool" a human into believing it was human.
The Turing test is a behavioral approach to determining whether a system is intelligent or not. Turing argued in a 1950 paper that conversation was the key to judging intelligence. In the Turing test, a judge has conversations (via teletype) with two systems, one human, the other a machine. The conversations can be about anything, and proceed for a set period of time (e.g., an hour). If, at the end of this time, the judge cannot distinguish the machine from the human on the basis of the conversation, then Turing argued that we would have to say that the machine was intelligent.
There are a number of different views about the utility of the Turing test in cognitive science. Some researchers argue that it is the benchmark test of what Searle calls strong AI, and as a result is crucial to defining intelligence. Other researchers take the position that the Turing test is too weak to be useful in this way, because many different systems can generate correct behaviors for incorrect (i.e., unintelligent) reasons. Famous examples of this are Weizenbaum's ELIZA program and Colby's PARRY program. Indeed, the general acceptance of ELIZA as being "intelligent" so appalled Weizenbaum that he withdrew from mainstream AI research, which he attacked in his landmark 1976 book.
The original Turing Test involved a human interrogator using a computer terminal, which was in turn connected to two additional and unseen, terminals. At one of the "unseen" terminals is a human; at the other is a piece of computer software or hardware written to act and respond as if it were human.
The interrogator would converse with both human and computer. If, after a certain amount of time (Turing proposed five minutes, but the exact amount of time is generally considered irrelevant), the interrogator cannot decide which candidate is the machine and which the human, the machine is said to be intelligent.
This test has been broadened over time, and generally a machine is said to have passed the Turing Test if it can convince the interrogator into believing it is human, without the need for a second human, candidate.
Turing recognized that the class of machines is potentially much larger than the class of discrete state machines, he was himself very confident that properly engineered discrete state machines could succeed in the Imitation Game (and, moreover, at the time that he was writing, there were certain discrete state machines -- “electronic computers” -- that loomed very large in the public imagination).
In 1991 Dr. Hugh Loebner started the annual Loebner Prize competition. A $100,000 prize is offered to the author of the first computer program to pass an unrestricted Turing test.
Reference:
- http://cogsci.ucsd.edu/~asaygin/tt/ttest.html#hi
|
|
Last updated on Sunday, 23rd November 2003, 10:01:51 AM.
Prof. Ashay Dharwadker
|
|

