| Home | Sign up! | Projects | Seminars | Research Notes | Today's Lecture | About |
Prakash PrasadEmail
olem82aero@hotmail.com
| Profile:
AIT Alumnus.
Undergrad Majors - Computer Science, Mathematics.
Computer Skills:
- Programming Languages
- AJAX
- C
- C++
- C#
- IBM PC Assembly Language
- Java
- Javascript
- Lisp
- Lex & Yacc
- Pascal
- Perl
- Prolog
- Python
- VB .net
- Web Design
- Databases
- Computer Graphics
- Adobe Photoshop CS2
- DirectX
- OpenGL
- POV - Ray
- Misc
I am a Gaming Fanatic and a big fan of the Need for Speed Series. I like almost all other racing games and a couple of first person shooter games.
Another big hobby of mine is to follow some of my favourite sports - Formula 1, Soccer & World Rally Championship.
A huge Liverpool FC fan. And Steven Gerrard is GOD. The guy seems to win important matches single-handedly.
I have given many Seminars during my stay at AIT, and have many more ideas. I am always intrigued by new stuff.
Prof. Ashay Dharwadker's Courses (3): | Course | Semester | Grade | | | Probability & Statistics | Spring 2003 | View | | | Algorithm Design - I | Fall 2002 | View | | | Algorithm Design - II | Spring 2004 | View | |
|
Project ID: 2
Course: Algorithm Design
Topic: Koch Star
| Description: One of the simplest examples of a fractal is the Koch Star.
- We start with an equilateral triangle.
- Then, each segment is divided into three equal parts,
- An equilateral triangle is constructed over the middle part, and
- Finally, the middle part is removed.
This process is repeated for all the resulting segments, ad infinitum. The result is the Koch Star fractal.
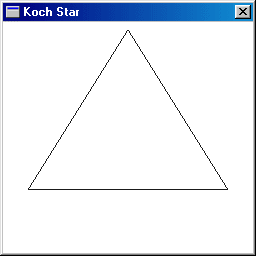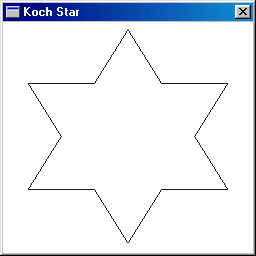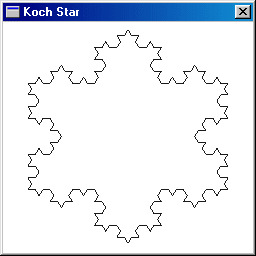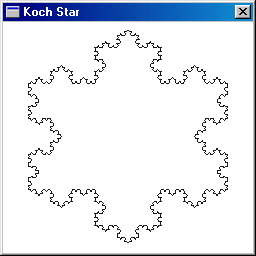
One strange observation is that the length of the boundary of the Koch Star is infinite, reasoning as follows - Suppose each segment of the initial triangle is of unit length so that the length of the boundary is 3. Then the subsequent lengths of the boundaries are 3(4/3), 3(4/3)2, 3(4/3)3, ... Hence, the length of the boundary of the Koch Star is the limit of 3(4/3)n as n approaches infinity, which is infinite. |
Project ID: 13
Course: Algorithm Design
Topic: Long Numbers
| Description: Any programming language, including C++ (any compiler) and Java, has constraints when it comes to using numbers. There is even a limit to numbers one can store in a double Data-type.
So, what's the solution? A very simple one is to create one's own numbers.
That's not too difficult. Just store all the digits in a string. Then, convert them into numbers and store them in arrays (or even better Vectors).
But the difficult part is to do basic arithmatical operations on these numbers.
But its not all that difficult. Believe Me. |
Project ID: 44
Course: Algorithm Design - II
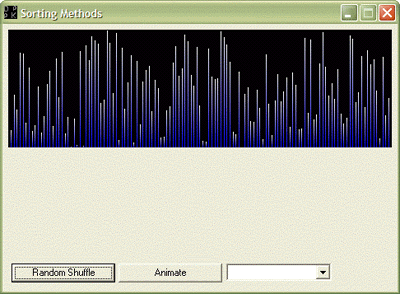
Topic: Sorting Algorithms Visualization
| | Description: My part of the project was to integrate every basic thing that the rest of
the group created into the Win32 environment using Visual C++. This is not a
very easy task since I am working in the VC++ Environment for the first time.
Team Manifesto
The first (and probably the most important) thing that any computer
programmer learns are the various algorithms for SORTING
data. They are absolutely critical for a complete understanding of the
whole computer science field itself. But it can get quite confusing at
times. Especially, when one wants to understand how each one of them
works? Or, How each one of them is different from the other?
We think we have an answer to that. Suppose you wish to introduce
somebody to the game of FOOTBALL. A verbal discription would not be very
helpful. The best solution would be to show a visual of the football game to
that person.
Same is the case with Sorting Methods. Through this project, we give a
visual discription of the various Sorting Algorithms, with the aim of
making learning easy and fun.
But the solution also gives rise to a more complex problem. How do we
represent the sorting algorithms visually. The solution is to create
unique visualization schemes to represent the status of
data elements at various instances of time.
This method of representation gives rise to a more complex field in
mathematics known as Dynamical Systems.
After the main idea of the project was concieved, the elements of the
project were distributed to the various team members.
Team Members:
- Karan Sahni (Algorithms - Coding Sorting Algorithms into C++ Programs)
- Parul Yadav (Visualizations - Creating Visualization Schemes in OpenGL)
- Devina Sibal (Visualizations - Creating Visualization Schemes in OpenGL)
- Prakash (Win32 Integration - Integrating all components in Visual C++ Environment)
|
Seminar ID: 2
Course: Probability and Statistics
Topic: Buffon's Needle
| Description: Buffon's
needle is a classic experiment in the field of Geometric Probability Theory.
A needle of length 1 is thrown on a floor made of planks of width 2. The
problem is to determine the probability p of the event that the needle
will fall across a crack between planks.
Using the geometry, we can calculate
p=1/p. We can also physically perform this experiment
or simulate it on a computer (see picture).

Suppose we throw the needle
N=160 times. We count the number of times M that the needle falls across
a crack between planks. In our computer simulation this event (red needle)
happened M=49 times and did not happen (blue needle) 111 times.
Hence,
M/N=p=1/p approximately. Now, to turn the mathematics
around, p=N/M=160/49=3.26531 giving us an approximation
for p !
This approximation is an example of
a general mathematical technique called the Monte Carlo Method.
|
Seminar ID: 45
Course: Algorithm Design II
Topic: Magic Squares
| Description: A Magic Square is an arrangement of the distinct positive integers 1, 2, ..., n2 such that the sum of all the rows, columns and main diagonals is always the same number.
This Number that all Rows, Columns and main Diagonals add upto is known as the Magic Constant.
The Magic Constant for an N X N Magic Square is represented by:
N ( N2 + 1 ) / 2
The logic behind this constant is very trivial and can be deduced by anyone who knows the following formula:
N ( N + 1 ) / 2
Yes. It is the sum of the first N Natural Numbers. In a Magic Square, the numbers that can be used are 1, 2, 3, ....... , N2. Since we have the first N2 Natural Numbers, the sum of the whole magic square is:
N2 ( N2 + 1 ) / 2
Also, the sum of each row (or column) is going to be same. Let it be x. Then the total sum of the Square will be N*x. This has to be equal to the total sum calculated above. So, the sum of numbers in each row (and hence, each column) is:
Total Sum / N = MAGIC CONSTANT
All the 8 possible 3 X 3 Magic Squares are given below:

* The above Magic Squares have been generated by using a Brute Force Algorithm which goes through all possible permutations ( which is very big - 9! = 362880 ; the next one for 4 being 16! = 20922789888000).
|
Seminar ID: 50
Course: Algorithm Design - II
Topic: The Mandelbrot Set
| Description: The Mandelbrot set was named after the mathematician Benoit Mandelbrot. The Mandelbrot set is one of the most famous examples of a fractal and the process of generating it is based on an extremely simple equation involving complex numbers.
The Mandelbrot set is a set of complex numbers, so we graph it on the complex number plane. However, first we have to find many numbers that are part of the set. To do this we need a test that will determine if a given number is inside the set or outside the set. The test is based on the equation:
Z = Z2 + C
C represents a constant number, meaning that it does not change during the testing process. C is the number we are testing; the Point on the complex plane that will be plotted when testing is complete. Z starts out as zero, but it changes as we repeatedly iterate this equation. With each iteration we create a new Z that is equal to the old Z squared plus constant C. So the number Z keeps changing throughout the test.
As we iterate our equation, Z changes and the magnitude of Z also changes. The magnitude of Z also changes. The magnitude of Z will do one of two things. It will either stay equal to or below 2 forever, or it will eventually surpass two. Once the magnitude of Z surpasses 2, it will increase forever. In the first case, where the magnitude of Z stays small, the number we are testing is part of the Mandelbrot set. If the magnitude of Z eventually surpasses 2, the number is not part of the Mandelbrot set. As we test many complex numbers we can graph the ones that are part of the Mandelbrot set on the complex number plane. If we plot thousands of points, an image of the set will appear as something depicted below:

|
Seminar ID: 56
Course: Algorithm Design II
Topic: N Queens Problem
| Description: In chess, a queen can move as far as she pleases, horizontally, vertically, or diagonally. A conventional chess board has 8 rows and 8 columns. But when a mathematician looks at a problem like this one, then he always likes to generalize it. The standard N by N Queen's problem asks a very interesting question - how to place N queens on a N by N chess board so that none of them can hit any other in one move.
Although solutions can be found by construction for N=1 and all N>3, many researchers have tried to find solutions by different methods with different success to demonstrate the properties of the methods (divide and conquer, search methods, neural networks). The following table summarizes what the authors have achieved.
| Author |
Method |
Max. N Solved |
Year |
| Gauß, Nauck |
trial and error |
8 |
1850 |
| several |
systematic construction |
all N>3 |
>1850 |
| Stone, Stone |
depth first search |
96 |
1987 |
| Page, Tagliarini |
Hopfield network |
10 |
1987 |
| Kajura, Akiyama, Anzai |
Boltzmann machine |
1000 |
1989 |
| Adorf, Johnston |
GDS |
1024 |
1989 |
| Abramson, Yung |
divide and conquer |
all N>39 |
1989 |
| Sosic, Gu |
local search, conflict minimization |
3000000 |
1990 |
| Chen, Wu |
Parallel PROLOG |
? |
1991 |
| Nakagawa, Kitagawa |
SDNN |
3000 |
1991 |
| Miller |
depth first search |
64 |
1992 |
| Shagrir |
Hopfield Network |
100 |
1992 |
| Mandziuk, Macukow |
Hopfield Network |
8 |
1992 |
| Mandziuk |
Hopfield Network |
80 |
1995 |
| Ali, Turner, Homifar |
Genetic Algorithm |
200 |
1992 |
| Minton, Johnston, Philips, Laird |
heuristic repair |
1000000 |
1992 |
| Takefuji |
Minimum network |
100 |
1992 |
| Lorenz |
GDS |
6001 |
1993 |
| Schaller |
DBNN |
200 |
1994 |
All the four solutions to the 6 X 6 Queens Problem are given below (1 represents the presence of a Queen at the position, while 0 represents the absence of a queen):
 |
Seminar ID: 58
Course: Database Design
Topic: MySQL's Full-Text Search Feature
| Description: For anybody who wishes to make MySQL as the backend for a database driven website, here's a very cool application.
It's called the full-text search feature. And it is exactly what it sounds like. MySQL can, just by way of a query, prove to be a very powerfull "SEARCH ENGINE".
So, how do we do it? Let's get started, shall we......
Step 1: SETUP
Well, first of all you would need to install MySQL (of course). And then setup a database (I am taking it that you are already familiar with it). And then, create a table on which you can do the search.
OK........
So, for creating the table, here's the command:
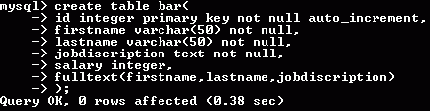
Remember, full-text search can only be implemented on fields of type varchar or text. The "fulltext()" keyword declares an instance of a fulltext index. You can create as many indexes in this manner as you wish (it can be helpful if you want to implement several search criterias, like by name or by job). Here, we will have only one criteria.
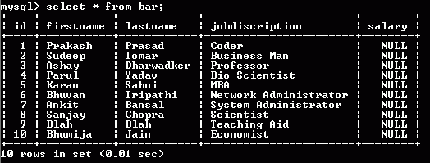
Now populate this table with more than 10 records, so that we can do some useful testing. "The more, the better", actually.

etc. Now test the table...
Step 2: USE
For using the feature, you just have to use this query....
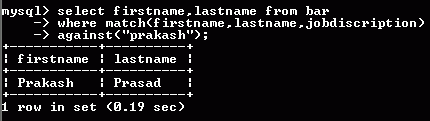
This query will return all the results which are related to "Prakash". The feature is NOT case-sensitive and has the ability to automatically remove "useless" words such as the, a, an, for, and etc.......
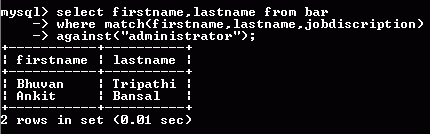
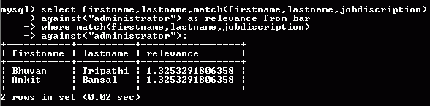
MySQL Full Text Binary Search
MySQL can also perform what is called full-text Boolean searches. It is a way to include or extract words and phrases from a search criteria. If you've ever searched for something like "+cricket -australia", then you've used a Boolean search engine. By combining operators, we can filter in/out words from our searches. Here are the various opertor rules:
- '+' indicates that this word must be present in every row returned.
- '-' indicates that this word must not be present in any row returned.
- By default (when neither + nor - is specified) the word is optional, but the rows that contain it will be rated higher.
- '<' '>' These two operators are used to respectively decrease or increase a word's contribution to the relevance assigned to a row.
- ( ) are used to group words into sub expressions.
- '~' cause's the word's contribution to the row relevance to be negative. A row that contains such a word will be rated lower than others, but will not be excluded altogether, as it would be with the '-' operator.
- * is the truncation operator and should be appended to the word, not prepended.
- A phrase that is enclosed in double quotes, matches only rows that contain this phrase, eaxactly as it was typed.
MySQL's Full-text binary search query looks something like this:
| select * from bar where match(firstname, lastname, jobdiscription) against ('+Prakash -MBA' in boolean mode);
|
This website also uses the full-text search feature for its search engine, simultaneously querying all its tables, for example try:
|
Research Note ID: 55
Course: Algorithm Design II
Topic: Prime Number Theorem
| Description: Properties of Prime Numbers have been studied as far back as the ancient Greek Civilizations.
Be it the mathematicians of Pythagoras' School (500 BC to 300 BC), Euclid in about 300 BC or
Eratosthenes in around 200 BC; the Greeks came up with most of the basic and important
identities and their proves:
- Pythagoras' Mathematicians came up with the identity of Perfect and Amicable numbers.
- Euclid, in the Book IX of the Elements, proved that there are infinitely many prime numbers.
- Eratosthenes devised a very fast algorithm for calculating primes called the Sieve of Eratosthenes.
Then there was a very long gap in the history of prime numbers during the Dark Ages.
But the work was again taken up by world famous mathematicians of the likes of Mersenne (Mersenne
Primes), Euler (extended Fermat's Little Theorem and found 60 pairs of amicable numbers),
Cataldi (proved M19 in 1588) , Fermat (Fermat's Little Theorem) , Legendre and Gauss.
Legendre and Gauss both did extensive calculations on the number of primes in a certain limit, i.e. ƒ(n) is the number of primes in the interval [1,n].
Gauss (who was a prodigious calculator) told a friend that whenever he had a spare 15 minutes he
would spend it in counting the primes in a 'chiliad' (a range of 1000 numbers). By the
end of his life it is estimated that he had counted all the primes up to about 3 million.
Both Legendre and Gauss came to the conclusion that for large n the density of primes
near n is about 1/log(n). A Graphical comparison between the actual value of π(n) and estimate ( n / log(n) ) is shown below:
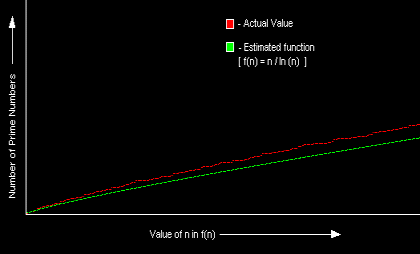
Legendre gave an estimate for π(n) the number of primes n of:
π(n) = n / ( log(n) - 1.08366 )
while Gauss's estimate is in terms of the logarithmic integral:
π(n) = ∫( 1 / log(t) ) dt where the range of integration is from 2 to n.
The statement that the density of primes is 1/log(n) is known as the Prime Number Theorem. |
Research Note ID: 80
Course: Machine Learning
Topic: Automatic Data Classification
| Description: Ever thought how google and other search engines give you the best result everytime? Of course, they classify the millions of webpages according to some criteria and produce the results according to the user's request. But, ever thought how tedious it could be to do that?
In order to classify data in a more dynamic manner, computer systems try to classify data (either webpages or Genetic data) into various classes. Many algorithms are used for this type of classification - Clustering Analysis, Perceptrons (Neural Networks), MaxSim's Formula, SVM (Support Vector Machine), SBC (Similarity Based Classification), HMM (Hidden Markov Model) etc.....
Though almost all of these algorithms are used very successfully to classify data, much is still desired from classification algorithms. For example:
- Every classification algorithm treats each set of data differently, i.e. the classifications by two algorithms of the same data may not be similar,
- There is no set standards on what kind of algorithm will work on what kind of data. It is only a matter of hit and try to figure out the "best fit", and
- All algorithms need a "decision parameter" with which they decide on the boundry seperating the various classes. This parameter has to be user defined and takes a lot of tweaking.
|
Research Note ID: 81
Course: Number Theory
Topic: Fibonacci Numbers
| Description: The Fibonacci Numbers are one of the most talked about numbers in mathematics.
The numbers were named after the person who introduced them the first time, Leonardo Fibonacci, a 12th Century Mathematician. He was also known as Leonardo of Pisa or Filius Bonacci.

The sequence was introduced in his book "The Liber Abaci" (1202).
The Fibonacci Numbers are a sequence of numbers where each term is the sum of the preceding two terms, with the first two terms being 0 and 1. It can be represented by the following formula: ƒ(n+2) = ƒ(n+1) + ƒ(n)An instance of the sequence is: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,......... |
Research Note ID: 82
Course: Number Theory
Topic: Random Fibonacci Series
| Description: As explained in my previous research note on Fibonacci Numbers, if a Fibonacci Series is represented by: ƒ(n + 2) = ƒ(n + 1) + ƒ(n)
Then, another interesting spin can be added by using this formula: ƒ(n + 2) = ± ƒ(n + 1) ± ƒ(n)
The sign makes the sequence very unpredictable. This is a "Random Fibonacci Series".
For a long time, this particular version of the fibonacci sequence was not considered to be of as much importance as the generic fibonacci sequence itself. But, recently mathematicians have been able to calculate the lim (n®¥) of the random fibonacci sequence with probability of the sign being Binomially Distributed with p = 1/2. |
Research Note ID: 83
Course: Number Theory
Topic: Golden Ratio
| Description: Ever imagined that every aspect of your life is controlled by Mathematics. If you haven't, then this better make you think.
When the concept of the Fibonacci Numbers was introduced, mathematicians the world over started working on the properties of these numbers. They soon found out the intresting property that the limit for the Fibonnaci series exists.
lim (n®¥) f(n+1)/f(n)
And what's even more interesting is that the value of this limit is the same as the legendary number that Euclid first talked about back in 300 BC - 1.61803399, or the GOLDEN RATIO. It has a lot of iteresting properties.
Now, did you ever think about that? |
Research Note ID: 85
Course: Individual Study
Topic: Magic Crystal Ball
| Description: A couple of days back, one of my friends told me to have a look at this "Magic" thing that is neat. I played around with it for sometime. It worked every single time. One of my friends doing it with me was in fact so mesmerized by this magic that he was convinced that the application can read his eye's co-ordinates of focus. Crazy I know, but what other explanation could there be. Here's the link, and please try it honestly for some time.
http://teluguone.com/funtime/index.jsp?filename=mindreader.htm

So I started to look for an explanation. Trying to decrypt the steps of the magic.
First, I need to pick a 2 digit number. That means that the number can be between 10 to 99 (including those numbers). Call it 'x'.
Second, I need to add the digits of these numbers. Call that 'y'.
Third, find (x-y) and then focus on the image corresponding to that.
Here, I found there might be some kind of mathematics involved. So, I wrote a small program that goes from 10 to 99, and calculates (x-y) for every value in the middle. That is how I solved this magic.
Now, you can go ahead and make "Magic" yourself and make a fool out of your friends who don't know about this.
|
|
Last updated on Thursday, 17th August 2006, 01:51:16 PM.
Prof. Ashay Dharwadker
|
|

